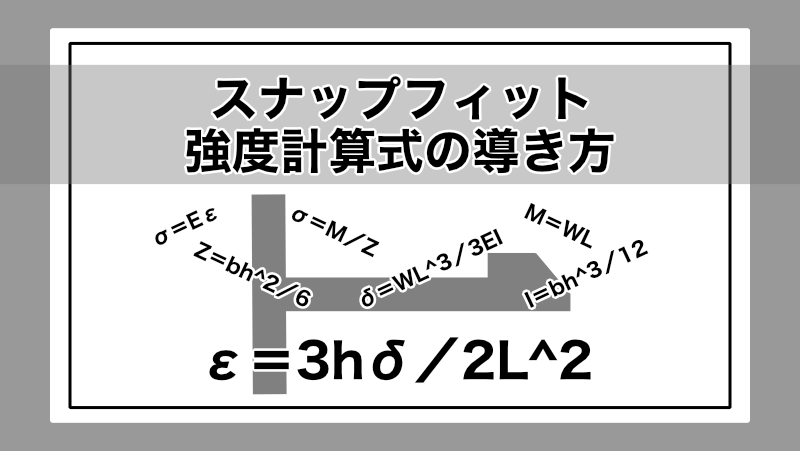
ひずみを使ったスナップフィット（嵌合つめ）の強度計算式「ε＝(3hδ)／(2L^2)）」は、成形品を設計する上で欠かすことのできない必須の計算式となっています。今回はそんな便利な計算式の導き方を、私の若かりし頃の記憶をたどり記録に残しておきたいと思います。見ていてまどろっこしいかもしれませんが、できる限り細かく手順を追いながら計算式を導いていく方法を Show Notes していきたいと思いますので、これを機にエンジニアとしての視野が少しばかりでも広がるきっかけにつながれば、私自身とてもうれしく思います。
----- スポンサーリンク -----
目次
Index
はじめに
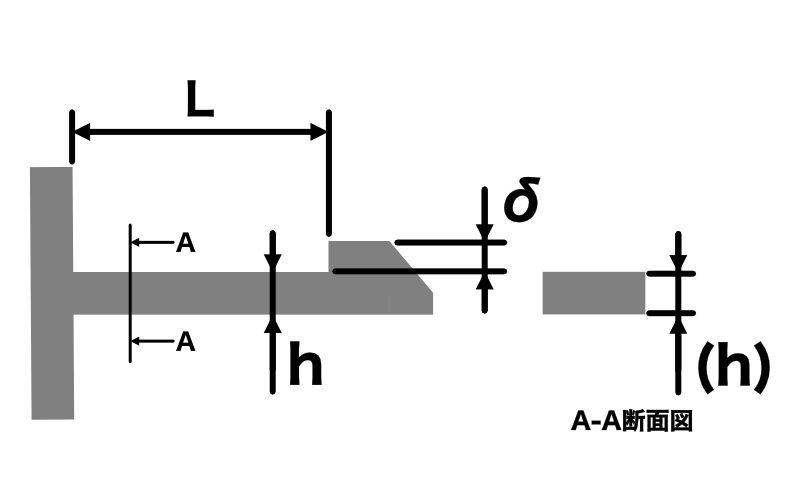
スナップフィット（嵌合つめ）の強度計算は、下記ひずみ（ε）の値を計算することで強度判定を行うことができます。
ε＝3hδ／2L^2
・ε：ひずみ
・h：板厚［mm］
・δ：たわみ量［mm］
・L：うでの長さ［mm］
このひずみを使ったスナップフィットの強度計算式ですが、フックの法則や片持ち梁の計算式により導き出されています。
丸覚えする必要はありませんが、計算式の導き方を知っておくことで、同じ計算を行うにしても、少し違った景色が見え自信につながるかと思います。
学生時代に教わった様々な計算式。
そんな代表的な計算式たちを組み合わせながら、スナップフィットの強度計算式を新米エンジニアだった頃の記憶をたどりながら導いていきたいと思います。
----- スポンサーリンク -----
ひずみを使ったスナップフィットの強度計算式の導き方
学生時代に材料力学などで教わった計6つの代表的な計算式を変換していくことで、ひずみを使ったスナップフィットの強度計算式を導くことができます。
代表となる計6つの計算式は下記のとおりです。
元となる6つの計算式
① σ＝Eε ・・・フックの法則
・σ：応力
・E：ヤング率（縦弾性係数）
・ε：ひずみ
② σ＝M／Z ・・・フックの法則
・σ：応力
・M：モーメント（トルク）
・Z：断面係数
③ M＝WL ・・・モーメントの計算式
・M：モーメント（トルク）
・W：荷重
・L：うでの長さ（梁の長さ）
④ δ＝WL^3／3EI ・・・片持ち梁のたわみ計算式
・δ：たわみ量
・W：荷重
・L：うでの長さ（梁の長さ）
・E：ヤング率（縦弾性係数）
・I：断面2次モーメント
⑤ I＝bh^3／12 ・・・断面2次モーメント（うでの断面形状が長方形の場合）
・I：断面2次モーメント
・ｂ：うでの幅
・ｈ：うでの厚み
⑥ Z＝bh^2／6 ・・・断面係数（うでの断面形状が長方形の場合）
・Z：断面係数
・ｂ：うでの幅
・ｈ：うでの厚み
それでは①〜⑥の計６つの計算式から、ひずみを使ったスナップフィット（嵌合つめ）の強度計算式を導いていきます。
----- スポンサーリンク -----
ひずみを使ったスナップフィットの強度計算式に変換する手順
手順1
「① σ＝Eε」を ”ε” の計算式へ変換する
σ＝Eε
↓（両辺を ”E” で割る）
ε＝σ／E
----- スポンサーリンク -----
手順2
「② σ＝M／Z」の ”M” に「③ M＝WL」を代入する
σ＝M／Z
↓ （”M” に、③式の ”WL” を代入する）
σ＝WL／Z
手順3
「④ δ＝WL^3／3EI 」を ”E” の計算式に変換する
δ＝WL^3／3EI
↓ （両辺に ”3EI” を掛ける）
3EIδ＝WL^3
↓ （両辺を ”3Iδ” で割る）
E＝WL^3／3Iδ
----- スポンサーリンク -----
手順4
手順1で変換した計算式「ε＝σ／E」の ”σ” と ”E” に、手順2と手順3で変換した ”WL／Z” と ”WL^3／3Iδ” を代入する
ε＝σ／E
↓（”σ” と ”E” に、手順2と手順3で変換した ”WL／Z” と ”WL^3／3Iδ” を代入する）
ε＝(WL／Z)／(WL^3／3Iδ)
↓（下線部の分子と分母を入れ替えて１つの分数にまとめる）
ε＝(WLｘ3Iδ)／(ZｘWL^3)
↓（分子と分母にある ”W” と ”L” を消し込む）
ε＝(3Iδ)／(ZL^2)
手順5
手順4で変換した計算式「ε＝(3Iδ)／(ZL^2)」の ”I” と ”Z” に「⑤ I＝bh^3／12」と「⑥ Z＝bh^2／6」を代入する
ε＝(3Iδ)／(ZL^2)
↓（分子の ”I” に ”bh^3／12”、分母の ”Z” に ”bh^2／6” を代入）
ε＝(3ｘ(bh^3／12)ｘδ)／((bh^2／6)ｘL^2)
↓（分子と分母内を整理）
ε＝(3bh^3ｘδ／12)／(bh^2ｘL^2／6)
↓（下線部の分子と分母を入れ替えて１つの分数にまとめる）
ε＝(3bh^3ｘδｘ6)／(12ｘbh^2ｘL^2)
↓（分子と分母にある ”整数” と ”bh” を消し込む）
ε＝(3hδ)／(2L^2) ・・・スナップフィットの強度計算式
以上でスナップフィットのひずみを使った強度計算式を導くことができました。
最後に
フックの法則や片持ち梁のたわみ計算式といった代表的な計6つの計算式から、ひずみを使ったスナップフィットの強度計算式の導き方についてご紹介しました。
冒頭でもお伝えしましたが、全ての計算式を丸覚えする必要はまったくありません。
エンジニアとして大切なことは、これらの計算式をいかに実用的に使っていくかということです。
計算式をたくさん知っていても、使わなければ単なる宝の持ち腐れとなります。
ひずみを使ったスナップフィットの強度計算式は、「ε＝(3δh)／(2L^2) 」といった極めてシンプルな計算式となっています。
他に登場した変数、すなわち「W（荷重）」、「E（ヤング率）」、「ｂ（うでの幅）」といった値は必要なく、「δ（つめの高さ）」、「h（うでの厚み）」、「L（うでの長さ）」といった、たった３つの単純な値だけで、強度計算を行うことができるのです。
当然このレベルの強度計算であれば、現在主流になっている解析ツールを使う必要はありません。
解析を行うための物性値の入力やメッシュを切る作業、拘束条件の設定といった一連の儀式を行なっている間に、今回ご紹介したひずみを使ったスナップフィットの強度計算式を使う方が、明らかに早く検証が完了するのは言うまでもありません。
解析は解析の持ち味。今回ご紹介したような手計算は手計算ならではの持ち味。
メリハリを効かせた使い分けのできるエンジニア。
これからもそんなエンジニアになれるよう、心がけていきたいものです。
