正弦波振動試験│加速度 振幅 周波数に関する計算式

はじめに

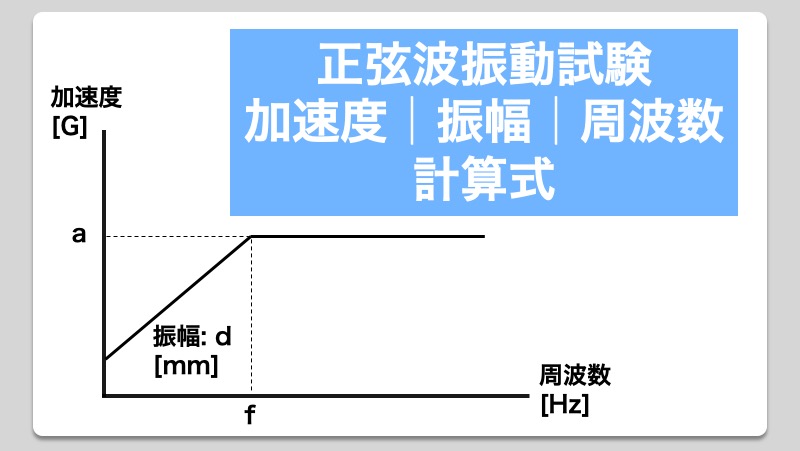
正弦波振動試験方法（JIS C 60068-2-6: 2010 / IEC 60068-2-6: 2007 ）における「加速度」、「振幅」、「周波数」に関する計算式を記載します。試験中にトラブルが出た際の糸口や、振動試験機の条件設定（折れ点周波数の計算など）の際にも役立つので、ぜひ活用してください。

計算式

正弦波振動において、「加速度」、「振幅」、「周波数」の間には、以下の関係が成立します。

この計算式を変形させることで、求めたい各数値を計算することができます。

※注意
振幅ですが、全振幅と片振幅といった2つの表現があります。片振幅を2倍したものが全振幅となります。逆に全振幅の半分が片振幅となります。混同せずに適切な値を使うよう注意してください。

「加速度」を求める計算式

※上記計算式と同じ

「振幅」を求める計算式

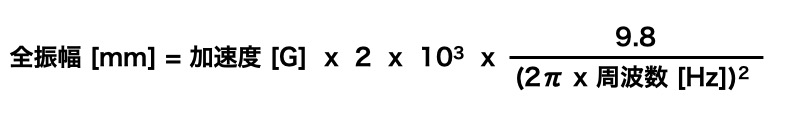
「周波数」を求める計算式

関連情報：ニュートンの運動方程式（F=ma）

振動条件において、自分の知りたいポイントの加速度が分かれば、あとは重量を知ることで力に換算することができます。（ニュートンの運動方程式）

上記計算式から力を知ることで、振動試験機に設置する治具（冶具）や製品の筐体などを設計する際の強度計算に活用することができます。
力はメカ的な感覚＝実感としてどれぐらいの外力が自分の知りたい部分に働いているのかいるのかが把握しやすくなるため、一見ごく単純な計算式であるものの、とても有用な計算式となっています。

最後に

製品開発における評価試験で振動は必須項目となっており、初試品でNGとなる場合が多々あります。
一般的に1軸2時間程度の計3軸といった長い試験時間ということもあり、試験開始後1掃引だけ見届けて、試験室からさっさと自分のデスクに戻ることが多いのではないでしょうか？
NGが発生した場合、どの時点でNGが発生したのかが、原因究明や対策にあたって、とても大きな手がかりとなります。もしトラブルが出た際は、ぜひ現物と向き合うようにしてください。（試験室にこもってください。）「三現主義」という言葉もあります。遠回りに見えますが、結果的に一番の近道となるはずです。
いつものごとく少し熱くなってしまい話が逸れてしまいましたが、今回ご紹介した計算式から、なんらかの糸口に結び付くことができればとても幸いです。
最近ではワイヤレスイヤホンもあります。振動試験室に引きこもる際はノートパソコンを持ち込み、振動試験機の騒音に負けず自分の好きな音楽を聴きながら並行して試験レポートを仕上たり、メール対応といったちょこまか案件をうまくこなしながら頑張っていきましょう！
くれぐれも偉い人にイヤホンが見つかり叱られないように。。。（笑）