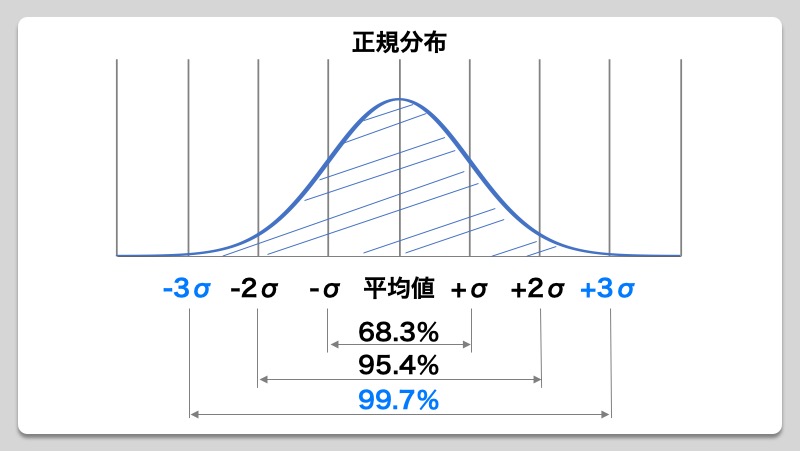
公差計算を行う際、MaxMinによるワースト値を用いた公差計算を行う方法と、統計学における正規分布の考え方を用いた公差計算を行う方法があります。前者のMaxMinによるワースト値と用いた公差計算は、最悪値をそのまま使っていることから、計算結果の値が100%担保されますが、常に最悪値を元に計算を行うため、過剰設計となりコスト高となります。一方で後者の統計学に基づいた公差計算方法は、より現実に即した考え方であり、設計寸法を正規分布の3σに投下して計算していくことで、計算結果の値を99.7%担保する形で計算を行うことできます。計算上0.3%の不良率（1,000台あたり不良3台）となりますが、MaxMinによるワースト値を用いた計算結果と比較し、公差を格段に緩和することができるため、過剰設計を抑え、加工精度も緩和できることから、結果的にコストダウンと量産性を高めることができます。今回はこの設計寸法を正規分布の3σに投下した、2乗和平方根を用いた公差計算方法について、ご紹介していきたいと思います。
----- スポンサーリンク -----
はじめに
Index
ものづくりをする上で、ジャストサイズに加工をすることはできません。例えばΦ30mmジャストの穴を開けようとしても、ドリル径や加工時のブレにより、30.2mmといった仕上がりになってしまうことがあります。そのため、設計者がここまでなら許せるといった許容範囲を「公差」という形で図面上に指示をしています。それらの公差を用いて設計検証を行い、その指示した寸法が妥当であるかを判断していくための計算方法を、例題サンプルを用いながら、これから一緒に計算を進めていきましょう。
目的
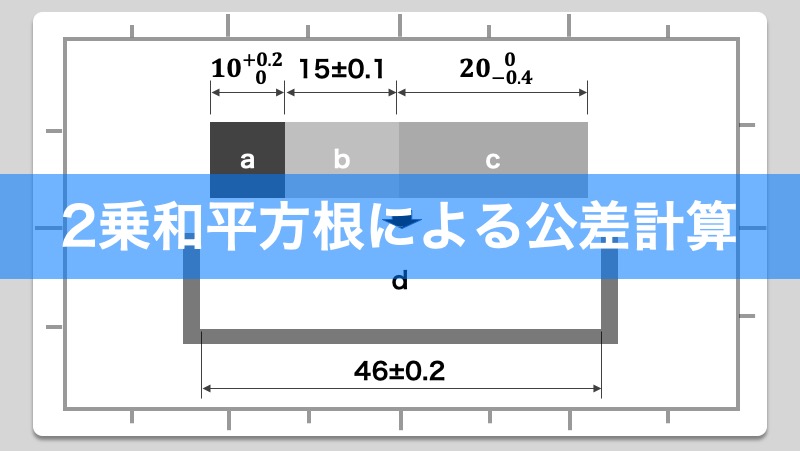
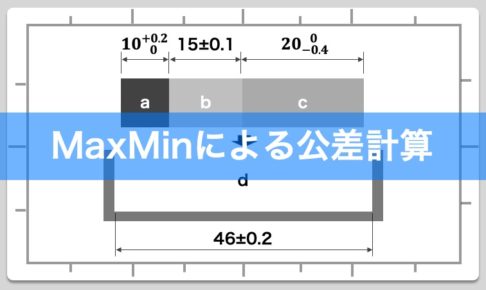
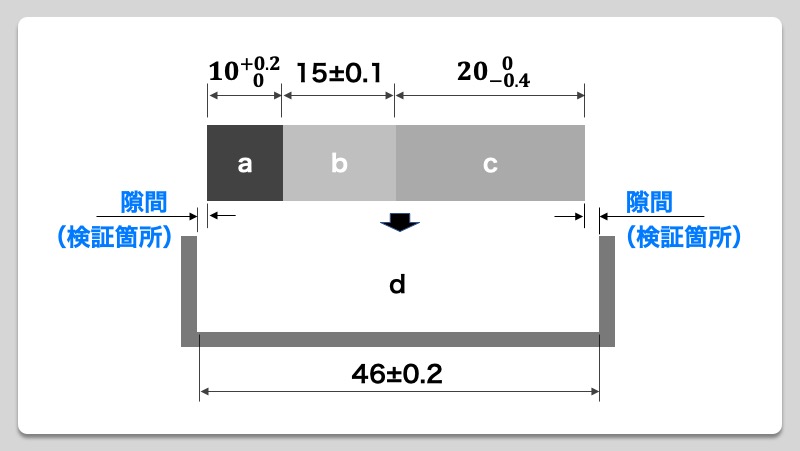
外部メーカーから購入してきた3つのブロック a、ｂ、ｃと、それらを収納するために新規に設計を行ったボックスdがあります。3つのブロックとボックスとの隙間について公差計算を行い、最悪時でも3つのブロックがボックスに干渉することなく収納できるかについて検証を行う。
----- スポンサーリンク -----
公差計算手順
公差計算を行う際、下記手順で進めることで誰でも簡単かつ効率的に計算をすることができます。メカエンジニアとなり軽く10年は経過していますが、このアプローチ方法でいまだに公差検証を行っており、これ以上の簡略化は難しいと思っています。この手順による公差計算方法を確実に習得し、公差計算をぜひ自分のものにしてください。
- 手順1：全て中間公差に換算する
- 手順2：検証用の図をつくる
- 手順3：いざ計算を行う
手順1：全て中間公差に換算する
片側公差と中間公差が混在している場合、計算が複雑となるため、全て中間公差に統一し、計算を行っていくのが効率的です。片側公差を中間公差化するため方法は単純かつとても簡単です。次の公式を使うことで、片側公差を中間公差に換算することができます。
今回の例題サンプルでは、aとcのブロックが片側公差で寸法が指示されています。これらを公式に当てはめると以下の計算式となり、中間公差に換算することができます。
----- スポンサーリンク -----
手順2：検証用の図をつくる
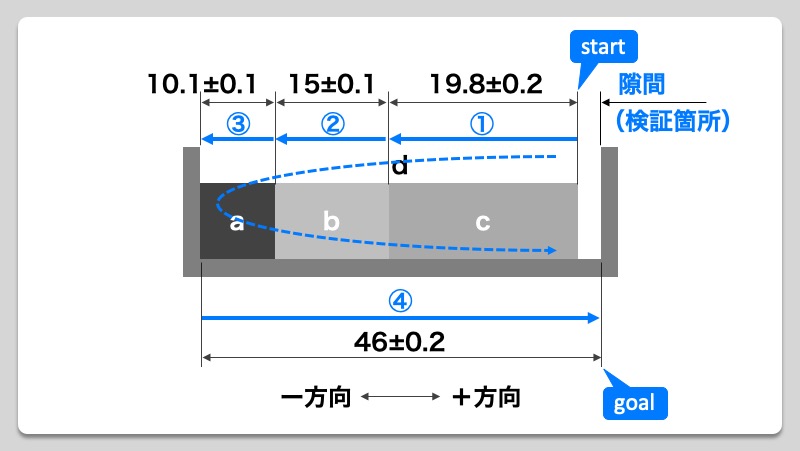
ここで改めて手順1で中間公差化した各寸法を検証図に当てはめていきます。その際、ボックスの左端からブロック敷き詰めていき、ボックスとブロックとの隙間が把握できるような検証図を作成していきます。自分が想像しやすいように隙間がより明確に把握できるよう、極端な検証図の作成をおすすめします。一例として以下のようなイメージとなります。
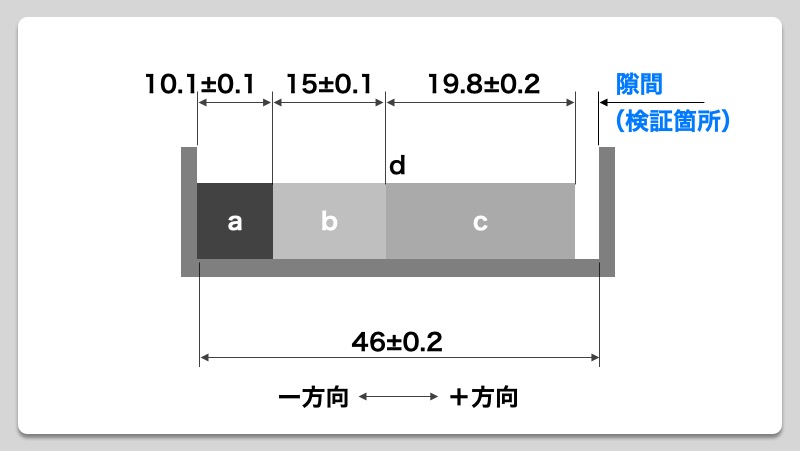
次にこの検証図に計算を行っていくためのループを形成していきます。公差計算は極めて単純で、足し算と引き算で答えを導くことができます。ループを作ることで差分すなわち隙間（検証箇所）を計算することができます。ループの作成方法は隙間（検証箇所）に対し「start」と「goal」を設定し、ループが形成できるよう各寸法が連なるよう順に①、②といったように番号を振り付けます。
手順3：いざ計算を行う
ここまでくれば、もう答えが出たも同然です。手順2で作成した検証図のループに従って①〜④の寸法を足し合わせ計算を行います。
基準寸法を足し合わせる際、＋方向と−方向に注意し、＋方向に進んで行く場合は＋、−方向に進んで行く場合は−を値の前に付けて計算を行うことで、差分すなわち検証寸法（隙間）を計算することができます。（公差については事前に全て中間公差化しているため、＋方向−方向といった概念はなく、単純に各公差の値を足し合わせていけばOKです。）
公差を足し合わせる際、2乗和平方根を使い正規分布の3σに投下し計算を行うことで、計算結果の値が99.7%の範囲内に入ることが統計学的に証明されています。
結論
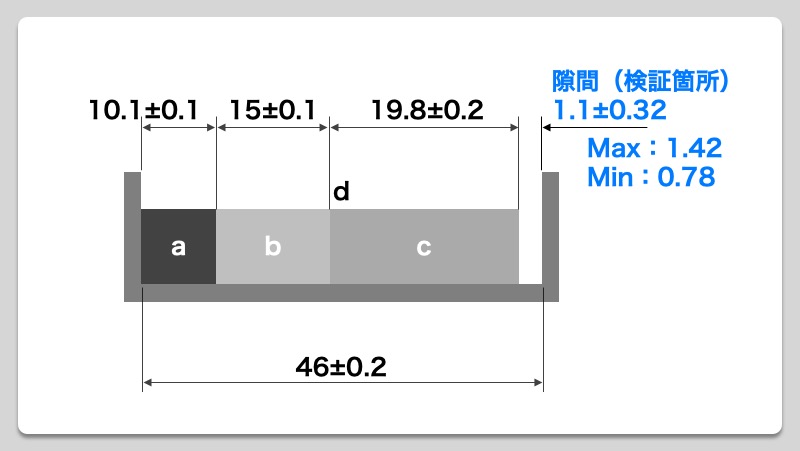
公差計算で算出した隙間（検証箇所）を検証図に当てはめると、下図のようになります。
----- スポンサーリンク -----
新規で設計を行ったボックス寸法（内寸）について
公差計算の結果、隙間（検証箇所）が最悪時、最大1.42mm、最小0.78mm になることが分かりました。最悪時でも隙間が最小0.78mm確保できていることから、ブロックとボックスが干渉することがないため、機能上問題なしと判断できます。
ボックスの最適寸法（内寸）について
隙間（検証寸法）が最悪時でも最小0.78mm確保できているということは、裏返せば収納ボックス寸法（内寸）を0.78mm小さくしても問題ないということが言えます。よって、収納ボックス寸法（内寸）を以下に改善することで、サイズダウンとコストダウンをはかることが可能です。
- From：46±0.2
- To：45.22±0.2 ≒ 45.3±0.2
----- スポンサーリンク -----
最後に
いかがでしたでしょうか。MaxMinによるワースト計算（全ての部品が最悪値で仕上がってしまうこと）は、現実的に見て本当に確率的に起こり得るのかといった考えから、多くの企業は統計学の考えをベースに計算を行っていることが一般的で、「2乗和平方根による公差計算」や「2乗和計算」、「3σによる公差計算」といった呼び方をしています。冒頭の繰り返しとなりますが、累積公差を2乗和平方根で計算することで、計算結果の値を99.7%担保する形で計算を行うことできます。計算上0.3%の不良率（1,000台あたり不良3台）となりますが、MaxMinによるワースト計算と比較し、公差を格段に緩和することができるため、過剰設計を抑え、加工精度も緩和できることから、結果的にコストダウンと量産性を高めることができます。ではすべての検証シーンにおいて、この計算方法をとってよいのでしょうか？ 答えは「No」です。少なからず、0.3％の不良率があるということと、加工方法によっては正規分布に投下できないケースもあることから、特に人命に関わるような検証シーンではMaxMinよるワースト計算を用いるべきシーンもあります。このあたりの使い分けは、各企業の考え方やエンジニアの経験により一概にこうだとは言い切れないため、ベテランエンジニアに相談の上、最適な公差計算方法を選択するようにしてください。
統計学に基づく考え方は、エンジニアにとって、とても強い味方となります。正規分布に関する今回の2乗和平方根と3σの関係など、深堀りすればするほど有用な情報が満載です。今回はごく一部分の紹介でしたので、またの機会を設け、別途紹介していきたいと思います。お楽しみに！
