【製品設計のいろは】MaxMinで公差計算を行うための3つの手順

エンジニアと一般の方との大きな違いをひとつだけ上げるとすれば、「エンジニアは最悪の場合でも設計の意図どおりに機能するものを作り上げている」ということが言えるかと思います。自動車や航空機をはじめ、特に人命に関わるものについては尚更で、何か最悪の状況が起こった場合、「想定外」といった一言で済ます訳にはいきません。今回はその礎となるメカエンジニアにとって基本中の基本となる公差計算について、これまでに得たノウハウを紹介していく形で説明していきたいと思います。

はじめに

ものづくりをする上で、ジャストサイズに加工をすることはできません。例えばΦ30mmジャストの穴を開けようとしても、ドリル径や加工時のブレにより、30.2mmといった仕上がりになってしまうことがあります。そのため、設計者がここまでなら許せるといった許容範囲を「公差」という形で図面上に指示をしています。それらの公差を用いて設計検証を行い、その指示した寸法が妥当であるかを判断していくための計算方法を、例題サンプルを用いながら、これから一緒に計算を進めていきましょう。

目的

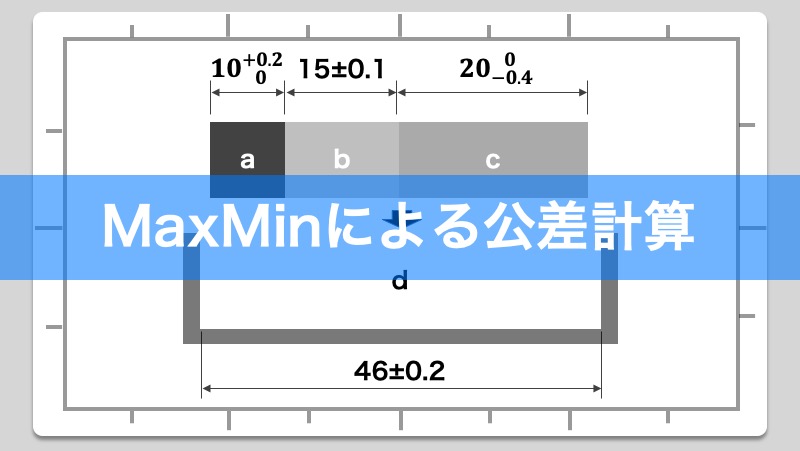
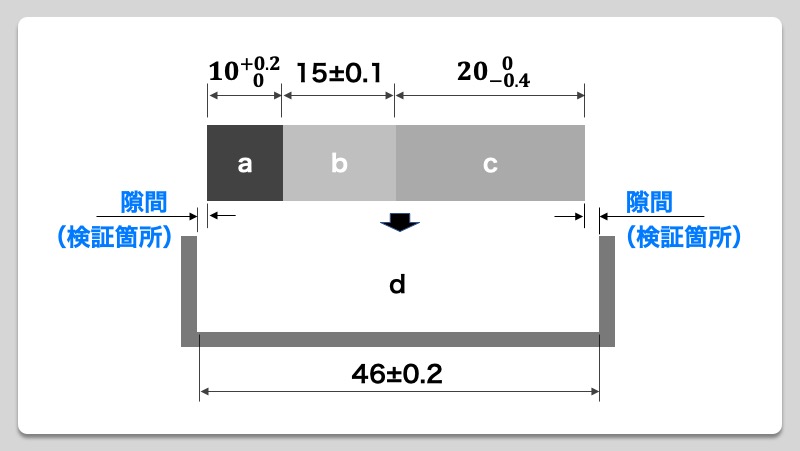
外部メーカーから購入してきた3つのブロック a、ｂ、ｃと、それらを収納するために新規に設計を行ったボックスdがあります。3つのブロックとボックスとの隙間について公差計算を行い、最悪時でも3つのブロックがボックスに干渉することなく収納できるかについて検証を行う。

計算手順

公差計算を行う際、下記手順で進めることで誰でも簡単かつ効率的に計算をすることができます。メカエンジニアとなり軽く10年は経過していますが、このアプローチ方法でいまだに公差検証を行っており、これ以上の簡略化は難しいと思っています。この手順による計算方法を確実に習得し、公差計算をぜひ自分のものにしてください。

手順1：全て中間公差に換算する

片側公差と中間公差が混在している場合、計算が複雑となるため、全て中間公差に統一し、計算を行っていくのが効率的です。片側公差を中間公差化するため方法は単純かつとても簡単です。次の公式を使うことで、片側公差を中間公差に換算することができます。

今回の例題サンプルでは、aとcのブロックが片側公差で寸法が指示されています。これらを公式に当てはめると以下の計算式となり、中間公差に換算することができます。

どうでしょう？ さほど難しくないですよね！

手順2：検証用の図をつくる

ここで改めて手順1で中間公差化した各寸法を検証図に当てはめていきます。その際、ボックスの左端からブロック敷き詰めていき、ボックスとブロックとの隙間が把握できるような検証図を作成していきます。自分が想像しやすいように隙間がより明確に把握できるよう、極端な検証図の作成をおすすめします。一例として以下のようなイメージとなります。

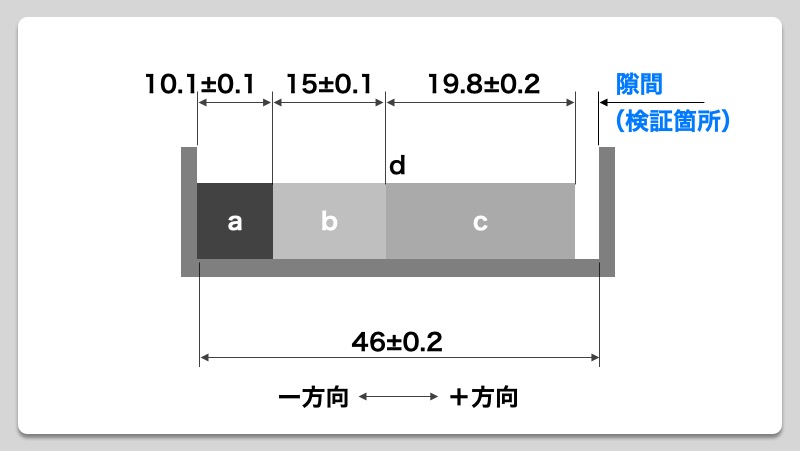
次にこの検証図に計算を行っていくためのループを形成していきます。公差計算は極めて単純で、足し算と引き算で答えを導くことができます。ループを作ることで差分すなわち隙間（検証箇所）を計算することができます。ループの作成方法は隙間（検証箇所）に対し「start」と「goal」を設定し、ループが形成できるよう各寸法が連なるよう順に①、②といったように番号を振り付けます。

検証図は綺麗に仕上げる必要はありません。自分の頭の中で計算ルートをイメージできるレベルの走り書きでOKです。ここまでで全てのお膳立てができました。あとは計算するのみです。おつかれさまでした！

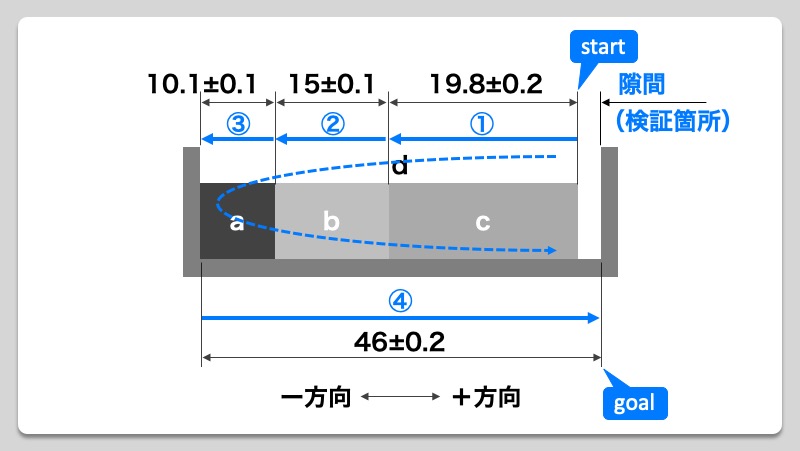
手順3：いざ計算を行う

ここまでくれば、もう答えが出たも同然です。手順2で作成した検証図のループに従って①〜④の寸法を足し合わせ計算を行います。基準寸法を足し合わせる際、＋方向と−方向に注意し、＋方向に進んで行く場合は＋、−方向に進んで行く場合は−を値の前に付けて計算を行うことで、差分すなわち検証寸法（隙間）を計算することができます。（公差については事前に全て中間公差化しているため、＋方向−方向といった概念はなく、単純に各公差の値を足し合わせていけばOKです。）

結論

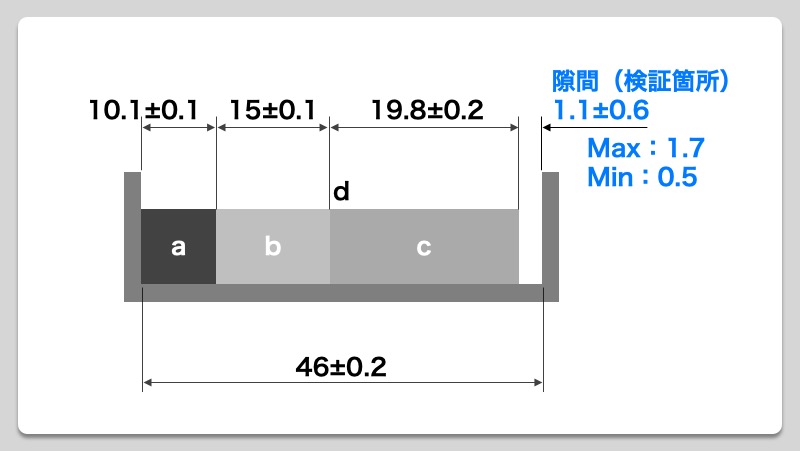
公差計算で算出した隙間（検証箇所）を検証図に当てはめると、下図のようになります。

新規で設計を行ったボックス寸法（内寸）について

公差計算の結果、隙間（検証箇所）が最悪時、最大1.7mm、最小0.5mm になることが分かりました。最悪時でも隙間が最小0.5mm確保できていることから、ブロックとボックスが干渉することがないため、機能上問題なしと判断できます。

ボックスの最適寸法（内寸）について

隙間（検証寸法）が最悪時でも最小0.5mm確保できているということは、裏返せば収納ボックス寸法（内寸）を0.5mm小さくしても問題ないということが言えます。よって、収納ボックス寸法（内寸）を以下に改善することで、サイズダウンとコストダウンをはかることが可能です。

• From：46±0.2
• To：45.5±0.2

最後に

いかがでしたでしょうか。公差計算というと、とても難し印象を持たれていた方が多かったと思いますが、ちょっとした「算数」と「ラフ図」を書くことができれば、誰でも計算することができ、エンジニアをしての一歩を踏み出すことができます。特にメカエンジニアの場合、直接目で見たり触れたりすることができるので、エレキやソフトと違い、とてもとっつきやすいかと思います。また計算が苦手な方も、学生の頃のように鉛筆と紙を使って計算する必要もなく、Excelをはじめとした計算ツールが自動的に計算してくれるので、鬼に金棒です。これであなたも最悪時を考慮した設計計算を行うことができました。おめでとうございます。これであなたもエンジニアの仲間入りです！ いかに最悪のシーンを想定し、事前に潰し込んでおけるか。それを実現するには経験と知識がものを言います。経験は残念ながら時間や環境といった自分でコントロールできない側面を持ち合わせていますが、知識については、しっかりと自分でコントロールし、着実に自分のものにしていくことができます。「想定外でした。。」と言うことのないよう、しっかりと準備しておきたいものですね。。。

準備とは「言い訳を排除する」こと

 

「ようするに “準備” というのは、言い訳の材料となり得るものを排除していく、そのために考え得るすべてのことをこなしていく、ということですね」

by イチロー