テストの結果や、身長や体重などについて、平均値で判断することが多いかと思います。例えば自分のテストの点数が80点でクラスの平均が60点だとします。この結果を受けて、「平均値より上回っているため安心!よかった!」といった経験をした方が多いのではないでしょうか。果たして本当に安心していてよかったのでしょうか? 今回は統計学による正規分布や標準偏差σを用いて、平均値による判断がいかに判断材料として不十分であるのかを、ご紹介していきたいと思います。
目次
Index
はじめに
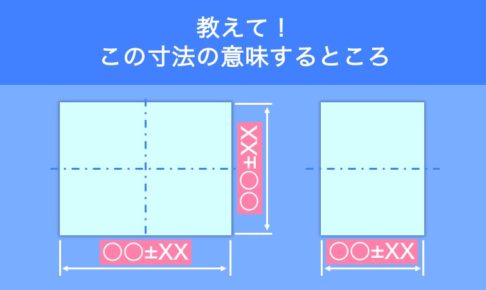
ある製品の一部に組み込まれる長さ「10±0.5」の棒を設計しました。狙い目が10mm、9.5mm〜10.5mmの範囲内となる長さで加工しなさいという内容です。この棒を製作するにあたり、購買担当がメーカー選定を行ったところ、2社が候補として上がりました。そこで購買担当が機転を利かせメーカーの実力を把握しておきたいという思いから、事前に試作を行いました。結果は下表のとおり。A社、B社ともに、加工長さが平均10mmといった設計者の意図する狙い目どおりの寸法に仕上がっており、両社とも加工に関する実力が同じという考えから、購買担当の知り合いがいるA社に決定したいとの申し入れがありました。果たしてこのままA社を採用してもよいのでしょうか? 今回はこのケースを例に検証をしていきたいと思います。
| A社 | B社 | |
| Q:品質 試作品カット長さ平均値(n=5) | 10.0mm | 10.0mm |
| C:コスト | @20円 | @20円 |
| D:納期 | 10日 | 10日 |
| 特記事項 | 知り合いがいる | 特になし |
後日、今回試作したサンプルの測定データが届きました。
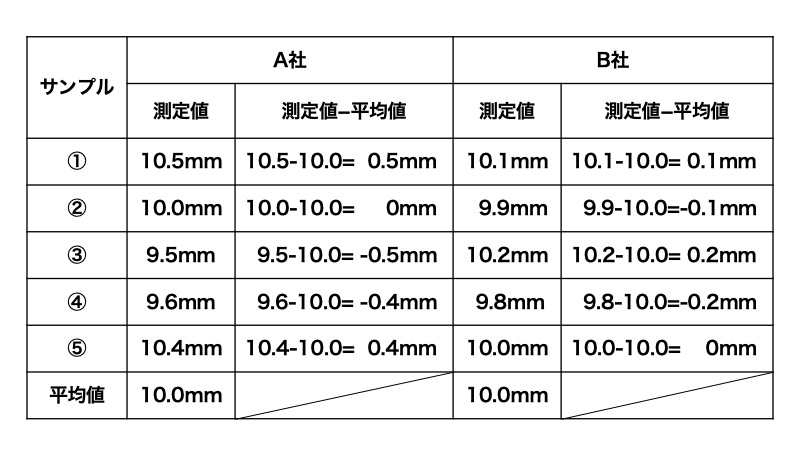
| サンプル | A社 | B社 |
| ① | 10.5mm | 10.1mm |
| ② | 10.0mm | 9.9mm |
| ③ | 9.5mm | 10.2mm |
| ④ | 9.6mm | 9.8mm |
| ⑤ | 10.4mm | 10.0mm |
| 平均値 | 10.0mm | 10.0mm |
正規分布と標準偏差σとは
同じような条件で生産したつもりでも、いろいろな条件が多少なりともばらついており、まったく同じ物はできません。
物のばらつきを品質特性として数値に表すことで、品質特性のばらつきといった形に置き換えることができます。
しかしそれは、まったくでたらめな値を取るわけではなく、一定のルールに従っていて、どのくらいの割合がどのくらいの割合(確率)で発生するかが決まっています。このルールを確立分布と呼んでおり、統計学的に数式で表すことができる正規分布になっていくことが分かっています。
この正規分布をを見てみると、中心付近の値が最も出る確率が高く、この中心値を平均値μ、中心付近をどの程度ばらつくのかを標準偏差σとして、以下のようなグラフで表されています。
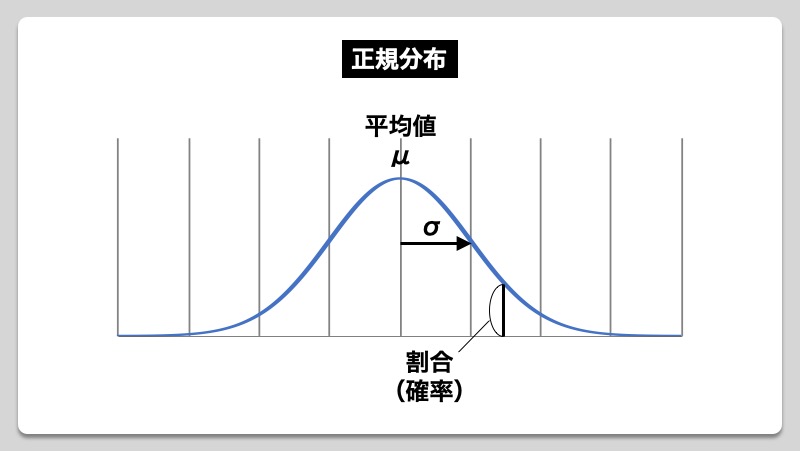
例えば、七夕のお願いごとをするために、長さ200mmの短冊を100枚用意するとします。ロール上に巻かれている細長い冊をセロハンテープのように引き出し、200mmを狙い目として次々とカットしていきます。カット後の100枚の短冊の長さを測定し、横軸を測定値、縦軸に個々の測定値に対する密集度を置いて、各データをプロットしていくと、正規分布の領域内に各測定値が分布する形となります。
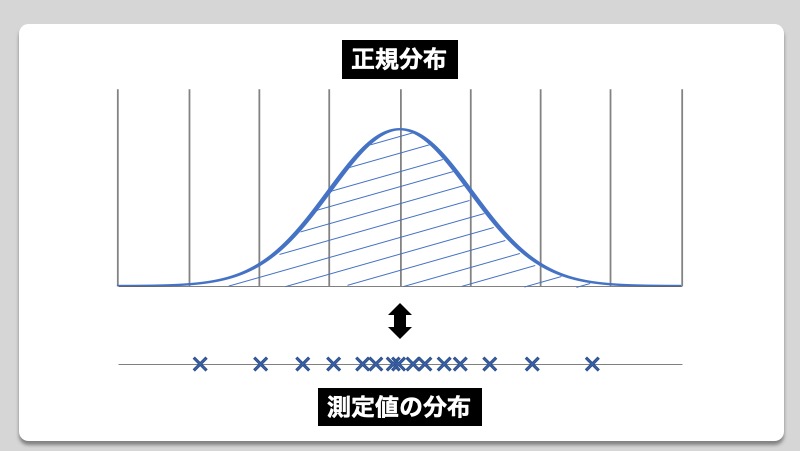
各サンプルのデータを統計学における正規分布の観点から考えた場合、得られた1枚の測定データが200mmから大きく外れていたとしても、残りの99枚全てが大きく外れているとは限りません。しかし、統計学の理論を利用することで、一部のサンプルを観測しただけで、その他のサンプルを含めた全体の姿を把握することができます。つまり、われわれが普段データとして得ているものをうまく使い、各データの集合体すなわち、その発生源である母集団全体を判断しようというのが統計的な考えとなっています。正規分布においてばらつく場合、中心となる平均値付近に対してどの範囲内にデータが入るのかといった確率は、以下のような性質になっていることが分かっています。
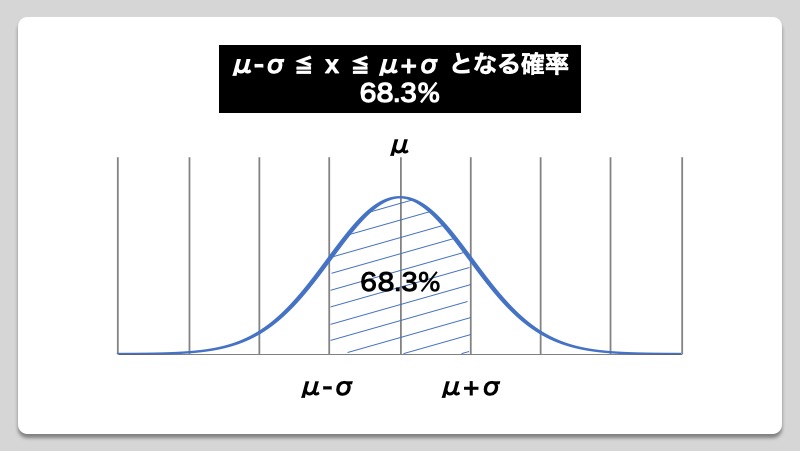
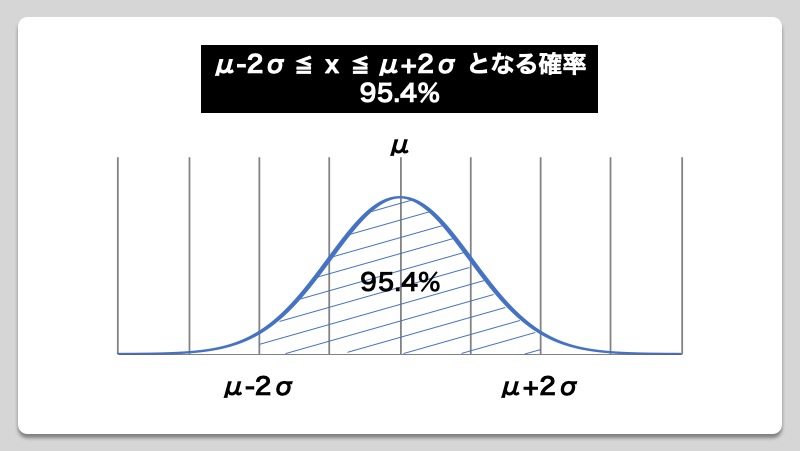
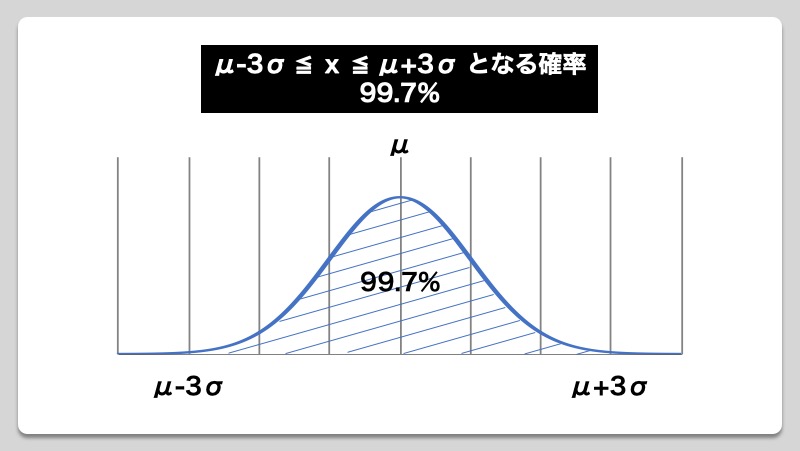
「±σ:68.3%」、「±2σ:95.4% 」、「±3σ:99.7%」といった3つの範囲がありますが、一般的にほぼ100%に近い「±3σ:99.7%」を用いて検証を行うことが多く、その場合の不良率は0.3%(1,000台で3台の不良)となりますが、ものづくりをする上でばらつきがある以上、要求寸法を100%満足させることは現実的に不可能であるため、「0.3%の不良率については許容しましょう」との考えがベースになっています。
それでは今回得られたA社、B社の測定データを元に、具体的に標準偏差σの計算を行い、両社の実力を確認していきましょう。また+αとして、3σの計算を行い、今後量産へ移行し大量生産をし続けても、99.7%の確率で設計要求寸法「10±0.5」を満足できるのか検証していきましょう。
3σを求めるための3つの計算手順
それでは下記3つの手順で、具体的にA社、B社の3σの値を求めます。
1. 各測定値から平均値を求める
2. 測定値と平均値を使って各サンプル個々のばらつきσを求める
3. 個々のサンプルのσを集約するために平均値を求め、3σを求める
Step1. 各測定値から平均値を求める
各測定値の平均値の求め方と計算結果は下記となります。

Step2. 測定値と平均値を使って各サンプル個々のばらつきσを求める
各サンプル個々のσの求め方は下記となります。

計算の結果、A社、B社の各サンプルの個々のσの値は、下表となります
Step3. 個々のサンプルのσを集約するために平均値を求め、3σを求める
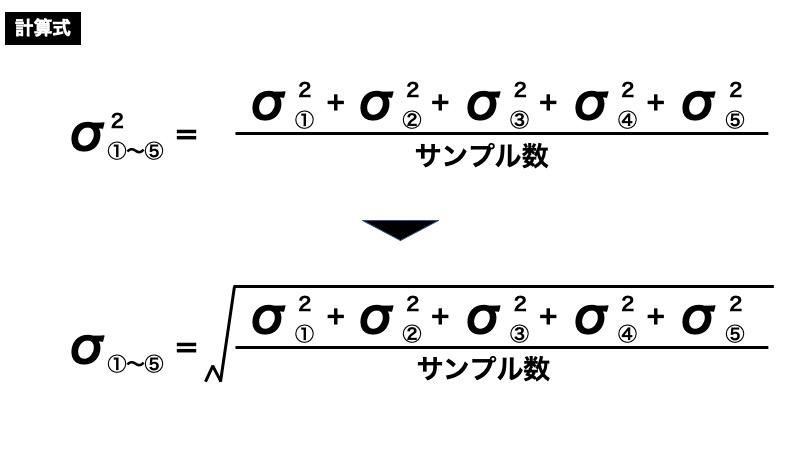
最終的なσの求め方は下記となります。
標準偏差σを2乗した値を分散と呼んでおり、統計学上、各サンプルのσの合算は、各分散を足し合わせることで計算することができ「分散の加法性」と呼ばれています。
この分散を合算した値をサンプル数で割り、平均をとることで、最終的なσを計算することができます。
その後、σを単純に3倍することで、3σを求めることができます。(99.7%の範囲内となるばらつきを求めることができる。)


結論
標準偏差σ(ばらつき)から見たA社、B社の実力比較
- 設計要求寸法:10±0.5
- 計算結果:
| A社 | B社 | |
| 平均値 | 10.0 | 10.0 |
| 標準偏差σ | 0.4 | 0.14 |
3σから見た、設計要求寸法と量産性について
- 設計要求寸法:10±0.5
- 計算結果:
| A社 | B社 | |
| 平均値 | 10.0 | 10.0 |
| 3σ | 1.2 | 0.42 |
今回計算で得た3σの値はつまり、平均値10.0に対するばらつき量を表しており、寸法に書き換えると以下のようになります。
- A社:10±1.2
- B社:10±0.42
最後に
いかがでしたでしょうか。通常は平均値でものごとの善し悪しを判断していることが多いと思います。例えば、駅へ向かう道中、信号待ちで立ち止まっている際、回りの人が一斉に空を見上げたとしましょう。自分も含め、まったく関係のない人も、同じように空を見上げる結果になるかと思います。平均値は、人間が本能的に持っている集団心理が働いてしまうことで、安心してしまい過信してしまう傾向にあります。世の中の事故やトラブルといったものは、人間の判断の誤りから引き起こすヒューマンエラーが全てといっても過言ではありません。その要因のひとつに、錯覚、すなわち思い込みといったものがあります。平均値は知りたい情報の傾向を掴むためにはとても有用な手段ではありますが、「平均値から大きく飛び出した値がある」ということ、「全体の傾向をすなわち分布で見た場合、自分の見たい値は果たして何%の領域に位置しているのか?」といった観点を付け加えることで、防ぐことのできる失敗や見えてくることが少なからずあるかと思います。今回ご紹介した統計学の手法を付け加え、失敗を防ぎ未来を予測することで、少しでも何かの役に立つようなことがあれば、とてもうれしく思います。