公差計算を行う際、計算結果の値が正規分布の ”3σ:99.7%” の範囲内となる考えを元に、各公差を2乗和平方根を用いた累積計算を行います。この2乗和平方根による公差計算ですが、過去に私が統計学の正規分布を少しかじり始めた頃、”3σ:99.7%” ではなく ”標準偏差σ:68.3%” の部分を計算しているように思え、疑心暗鬼に陥ったことが度々ありました。少し時間が空いてしまうとまた忘れてしまいそうなので、今回は「2乗和平方根はσではなく、3σとイコールなんだよ!」ということを記憶から記録に変えつつ、簡単な計算式を使いながらご紹介していきたいと思います。
「2乗和平方根」と「正規分布の3σ:99.7%」の関係性
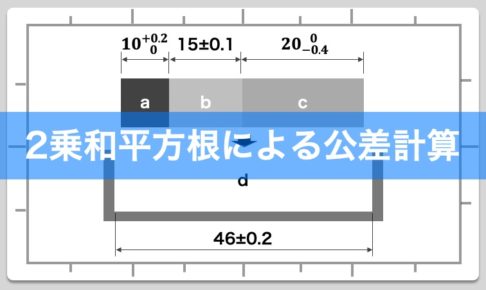
それでは下にある関連記事を例題に使い、2乗和平方根と3σの関係を追いかけていきたいと思います。
検証図と計算式を抜粋したものが下記となります。
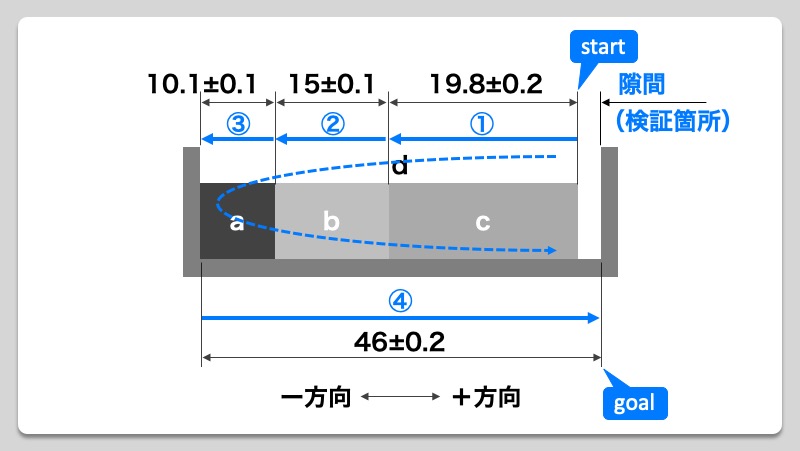

今回はこの計算式の中にある公差部分すなわち2乗和平方根の部分と3σがなぜイコールになっているのか、一緒に順を追いながら少しずつ見ていきましょう!
①〜④の各寸法の公差は以下となります。
①:0.2
②:0.1
③:0.1
④:0.2
①〜④の各公差を正規分布で言うところの「ばらつき」の部分として見なしたいので、この部分を3σに置き換えます。
①:3σ=0.2
②:3σ=0.1
③:3σ=0.1
④:3σ=0.2
最終的に上記①〜④の各3σの値を足し合わせることで、求めたい検証箇所の3σとなります。
統計学上、標準偏差σを2乗した値を分散と呼んでおり、標準偏差σの足し合わせは各分散を足し合わせることで計算することができます。(分散の加法性)
と言うことで、統計学上、標準偏差σを2乗した値(分散)でないと足し合わせできないため、①〜④の3σを標準偏差σに置き換えます。
①:3σ=0.2 → σ=0.2/3
②:3σ=0.1 → σ=0.1/3
③:3σ=0.1 → σ=0.1/3
④:3σ=0.2 → σ=0.2/3
これで準備OKです。
それでは、①〜④の標準偏差σを2乗した値(分散)を足し合わていきましょう!

以上の計算式から、3σが2乗和平方根とイコールとなっていることが分かりました。
おつかれさまでした!
最後に
いかがでしたでしょうか。2乗和平方根で公差計算を行い、その計算結果の値が統計学上の正規分布における ”3σ:99.7%” の範囲内になっていることを理解しつつも、さも当然のように公式として扱い計算を行っているかと思います。今回は公差計算を膨らませての話でしたが、その他の強度計算においても同様に、公式を使い、設計検証を行っているかと思います。もちろんその方法で問題はありません、型に当て嵌まらない案件が来た場合、いつもの直球だけで突破口を見いだせず、時には変化球を投げなければ次のステップに進まないような場面があります。変化球といった臨機応変に機転を利かせて行くには、経験や原理原則にもとづく知識の積み重ねがあってこそ、そこで初めて事を成し遂げることができます。そのためには「急がば回れ」ではありませんが、時にはあえて違う道を進むことで、後々振り返ると「貴重な経験だったなぁ」と思えることが多々あります。時にはふと漠然と、ごく当たり前のように思っていることを少し掘り下げて考えてみるといった機会や余裕、ぜひ作っていきたいものですね。。
いや、これからはぜひ一緒に作っていきましょう!